书籍 Grokking Deep Reinforcement Learning Chapter 2: Planning For Sequential Decision-Making Problems学习笔记
书籍www.manning.com/books/grokking-deep-reinforcement-learning?a_aid=gdrl

代码github.com/mimoralea/gdrl/blob/master/notebooks/chapter_02/chapter-02.ipynb

1 序列决策问题的结构我们回忆一下强化学习进行的交互循环。
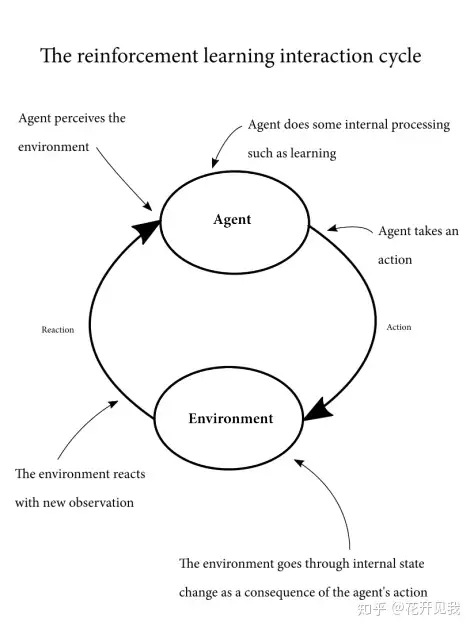
我们有一个序列决策问题,首先我们有环境(Environment)和智能体(Agent),环境是智能体不能完全控制的全部东西的集合,甚至包括了一些看起来像智能体一部分的东西例如,假设你是一个做决策的智能体,那么你的手是属于环境的而不是属于智能体的,因为我们希望做决策的智能体只负责做决策。
而你的手不做决策所以不是决策智能体的一部分智能体可以通过行动(action)影响环境行动可能会在环境中产生非确定性后果:可能在同样的状态下采用同样的行动的每次尝试会产生不同的结果在任意给定时间,环境会定义一个与决策者相关的变量配置,也就是状态(state)。
例如,一个股票交易agent它建立的环境状态为可用的现金数量,股价,日期,国家政治状况等等所有这些变量配置组成了单个状态当一个行动被agent发送给环境后,环境基于其内部状态,和这个行动,转移到一个新的状态。
这个内部状态,agent有可能可以完全获取,有可能不能完全获取比如打扑克这个游戏的环境就有一些变量就是not fully-observable(不完全可观察的),比如其他玩家手里的牌是什么在环境转移到新的状态时也对agnet的行动做出反馈,这个反馈对环境内在状态变化有了一些暗示,这就是agnet的观察(observation)。
除了observation,环境还给agent发送了一个张量被称之为奖赏(reward)。 奖赏是环境对上一个行动的评价。
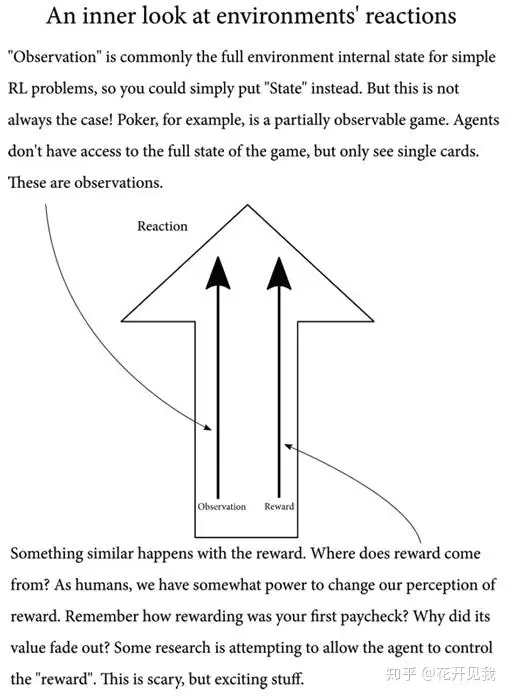
到现在为止,我们假设环境总是通过奖赏告诉智能体什么是好什么是坏奖赏可以是任意正负实数 一个智能体将使用这些部分:智能体采取行动之前的环境状态,智能体采取的行动,新状态,奖赏循环往复这些成分的组合:一个状态集合,一个行动集合,状态改变的表示,智能体行动序列返回的奖赏,组成了 Markov Decision Processes(MDP)框架。
现在我们以一个冰湖环境为例介绍MDP的各个部分。The Frozen Lake 环境介绍假设你要用MDP表示下面这个简单的格子世界, 叫 Frozen Lake也就是冰湖。
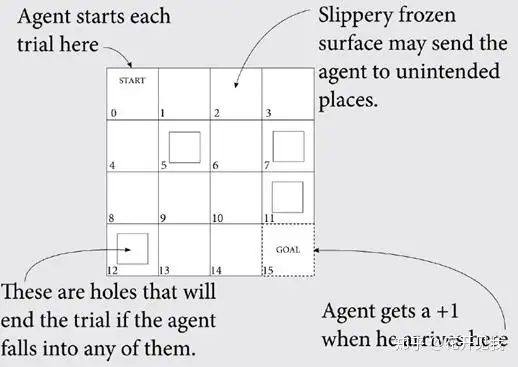
正如您所看到的,这个世界在任何时间步都有16个位置 智能体将在START 位置开始每个试验,也称为一集进入GOAL位置会环境给智能体+1奖励,当前这一集结束代理将再次出现在START位置中将开始下一集我们的这个网格世界的表面很滑。
智能体按预期移动概率为33.3333%,其余66.6666%将按直角方向均匀分配例如,如果智能体选择向下移动,则有33.3333%的可能性向下移动,33.3333%的可能性向左移动,33.3333%的可能性向右移动。
如果智能体试图移出这个格子世界,它将弹回到它原来的单元格世界上有四个洞(如图所示在5,7,11,12号格子上)如果代理人进入其中一个洞,则该集结束,智能体返回起始位置,并开始新的一集试验系统状态在这个冰湖环境显然总共有16 个状态. 我们把它们标记为0到15
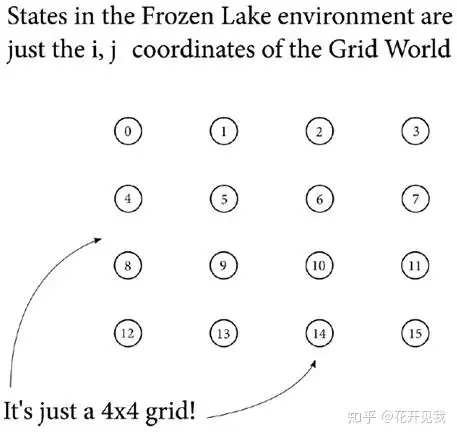
一个状态(state)就是一个自我包含的关于问题的配置我们定义系统的状态集合S, 比如这个冰湖环境,状态是离散的而非连续的,是有限的而非无限的,|S|=n每个环境状态都是所有必须变量的独特配置使其与其他状态区分开来。
比如在这个冰湖环境中,你只需要知道智能体的当前状态来预测下一个可能状态,而不管前面经历过的状态,比如你现在在状态2,你只可能转移到1, 3, 6不管你之前是从1,3, 6中的哪个状态转移到状态2的MDP的这种下一个时间步的状态,只取决与当前状态和行动,不记忆之前历史的特性被称为马尔科夫性:。
马尔科夫性
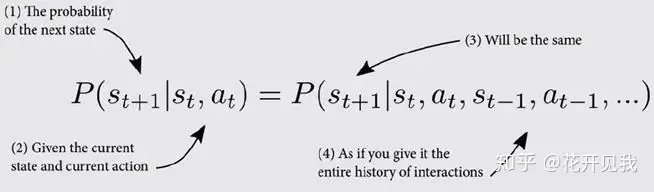
MDP中的全部状态集合记为S+, 其中有个子集被称之为初始状态或者起始状态,还有一个子集称之为终止状态或者吸收状态。在这个冰湖环境,只有一个初始状态,也就是状态0,有5个终止状态,示意图如下
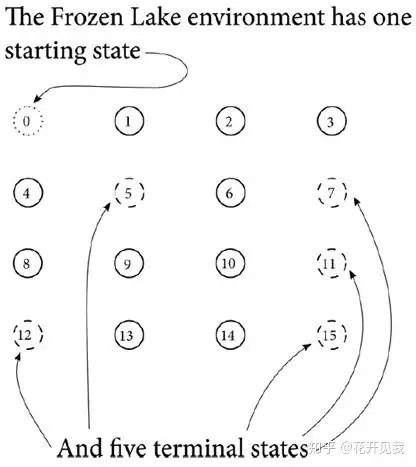
可以采取的行动在这个冰湖中,任意状态下智能体可以采取上下左右四个行动MDP中可采取的行动记为A,也是离散且有限的,大小为|A|=k行动是系统的公开API,智能体可以通过它推动系统往其想要的方向改变也有可能会有不被允许的行动,那么可以用A(s)函数表示状态s下可用的行动。
智能体可用通过决定性的方法也可用使用概率性的方法选择行动行动的结果在这个冰湖环境下我们知道我们的智能体有 33.3333%的机会真正按照我们想要的意图行进还有66.6666% 的几率延你想要的方向的直角方向运动.下图展示状态 6, 13, and 15 的转移函数。
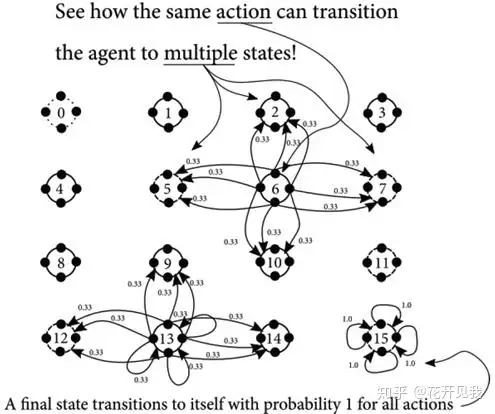

用表格表示的转移函数或者状态转移概率环境转移的方法可以称之为转移函数,或者状态转移概率表示为T(s, a), 转移函数T将状态s,与当前的行动a映射到新的状态强化信号在冰湖中,到达终点状态15时奖励函数返回+1 否则返回0.。
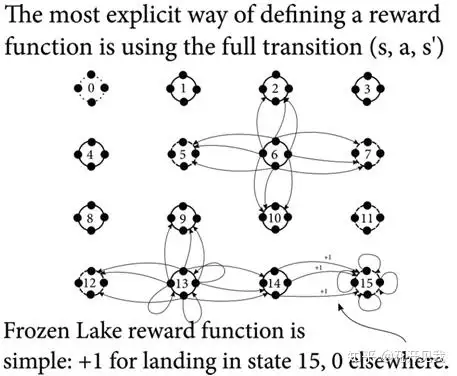
奖励函数分为r(s,a,s’) 与 r (s,a)
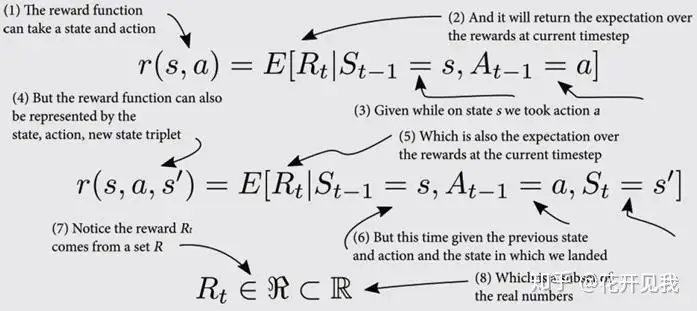
奖励函数把状态行动对(s,a)或者状态,行动,下一个状态对 (s,a,s’)映射到一个张量当奖励函数为正时我们称之为收益或者目标, 大部分问题都至少有一个正信号奖励为负数是我们称之为惩罚或者代价,在机器人相关的实践中我们常常需要代价,以便在有一定约束的情况下达到目标。
时间 我们必须在MDP中表示时间根据时间的不同任务可以分为下面两种:分集任务连续任务分集任务 是存在时间限制的任务,要么存在一个时间步数的限制,要么存在一个终止状态连续任务 则是一类永远持续的任务,没有时间步限制,也没有终止状态。
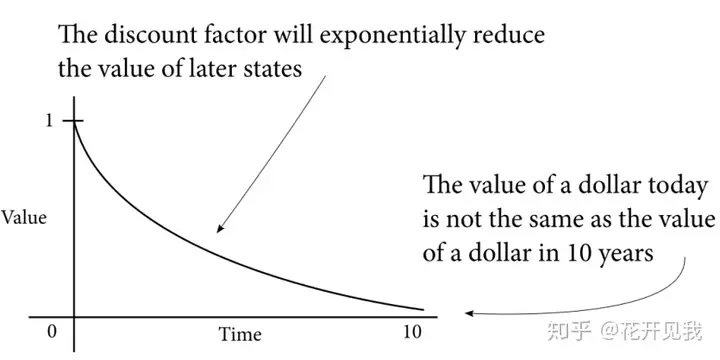
我们将从分集任务的开始到结尾的连续时间步序列称为一集或者一次试验,一个阶段gamma,也就是折扣因子由于在无限时间任务中可能存在无限的时间步数序列,我们需要一种方法来随着时间推移给奖励的值打折,告诉智能体越早获得正的奖励越好。
冰湖MDP这个世界有16个状态,4个动作,达到目标时,给出的唯一奖励是1有5个终端状态,其中4个是终止episode并且不给予奖励的洞,其中一个是目标状态(再次给予1个奖励)下面是用python dict 表示的这个MDP。

2 做决策智能体的目标现在我们开始想如何创建解决这个问题的智能体首先,我们需要定义解决这个问题的智能体,智能体采取一系列的行动,这个行动将在1个episode或者智能体的整个生命周期中最大化奖励的和。
智能体的整个运动轨迹的奖励集合称之为预期返回值 (expected returns)看起来我们需要的是一个计划也就是从起点到目标的一系列行动但这还不够!正如之前提到的,冰湖环境是随机的;采取的行动并不总是按照我们的意图行事。
如果由于环境的随机性,我们的智能体会到达我们计划外的区域这事,智能体需要是一项策略策略可以是随机的;该策略将状态映射到在状态下各个行动的选择概率也可以是确定性策略,该策略仅将状态映射到具体的行动上行动的策略
鉴于冰湖环境中的随机性,智能体需要找到一个政策,表示为π。策略是一个为任何给定的非终止状态返回行动的函数下图这是一个示例策略:
你可以直观地知道朝着目标的方向前进应该是对该状态采取的最佳行动。然而,我们需要一种更精确的方法,尤其是是考虑到冰湖环境的随机性。状态的价值
们怎样才能在数字上代表一个状态的价值?如果我们的代理人处于状态14(在目标的左侧),那么比在状态13(在14的左边)更好吗?而且它究竟有多好?我们把期望返回值定义为智能体最大化的未来奖励,我们现在定义遵循某个策略时一个状态的价值:如果代理遵循从状态s开始的遵循策略π的期望返回值就是,状态s在策略π下的价值。
此定义称之为状态价值函数,它仅表示智能体在给定环境状态并遵循给定策略时可能期望接收到的返回值。
采取一个行动的价值状态的价值取决于在该状态采取行动的价值因此,我们需要一种方法来比较在任何状态下采取任何行动的价值,以便我们能够确定最佳行动,从而提出最佳政策如果智能体遵循从状态s开始的策略π并采取行动a,期望返回值就是一个行动的价值函数。
采取一个行动的优势这是一种从前面两种价值函数衍生的一种新的价值函数,叫做优势价值函数,它是在状态s下采取行动a的行动价值函数减去状态s下遵循策略π的状态价值函数得到,优势价值函数描述了采取给定行动而不是遵循既定策略的价值。
最优策略,状态价值函数,行动价值函数和优势价值函数是我们用于描述,评估和改进行为的组件当这些组件是最好的时,我们称之为最优最优策略是期望返回值大于或等于所有其他政策的期望返回值的策略最佳状态价值函数是所有策略中具有最大值的价值函数。
最佳行动价值函数是所有策略中有最大值的行动价值函数您可能以及注意到,如果您具有最佳状态值函数,则可以简单地使用MDP执行一步搜索最佳行动值函数,然后使用它来构建最优策略